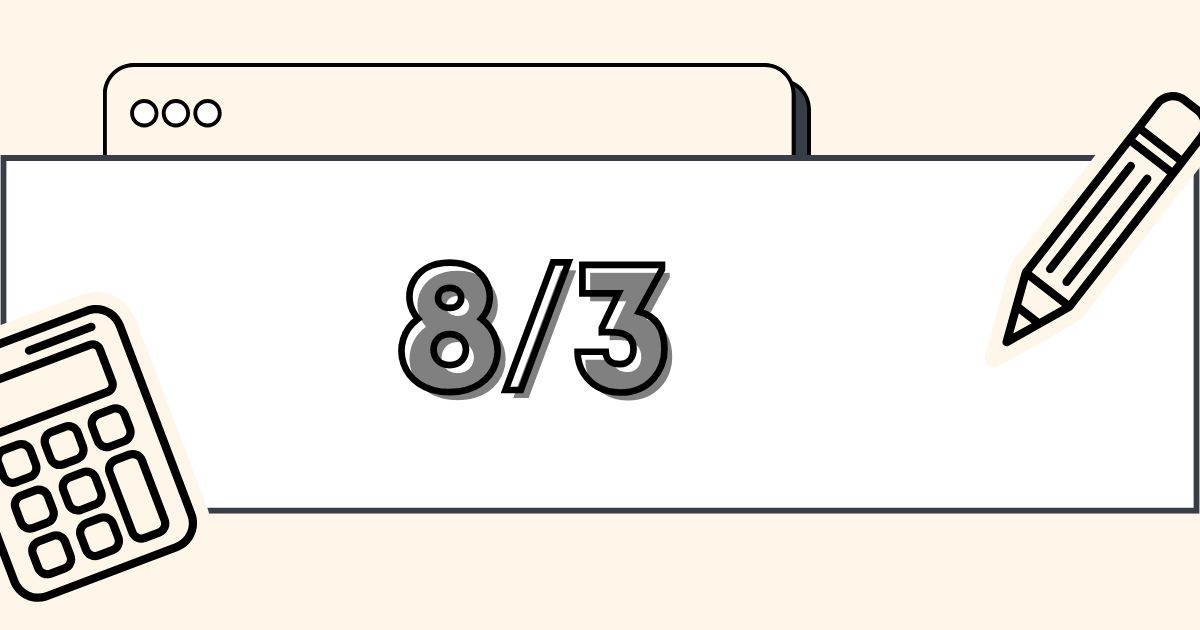
At its core, 8/3 is a simple fraction that equals approximately 2.666…, a repeating decimal. While it looks like a straightforward math expression, this fraction shows up in many unexpected places—architecture, cooking, budgeting, and even philosophy. Knowing how to interpret and use this kind of number can help in both professional and everyday scenarios.
The Decimal Representation of 8/3
Dividing 8 by 3 results in 2.666…, with the digit 6 repeating endlessly. This repeating decimal can also be written as 2.67 when rounded to two decimal places or kept as 2.66̅ to show its continuous nature. This matters more than you might think—especially in precise calculations.
Why 8/3 Is a Rational Number
A rational number is any number that can be expressed as the ratio of two integers. Since 8/3 fits this rule perfectly (8 and 3 are both whole numbers), it’s a classic rational number. Understanding this helps you grasp how math handles infinite decimals that repeat.
Real-World Uses of 8/3
If you’re baking and a recipe calls for 8 cups of flour divided among 3 cakes, you’re working with 8/3. Each cake would get 2 and 2/3 cups, and knowing how to work with this measurement helps avoid kitchen disasters. Similar logic applies to carpentry, DIY projects, or splitting quantities in budgeting.
Converting 8/3 to Mixed Numbers
In mixed number form, 8/3 becomes 2 2/3. This form is more relatable in real life—think of saying “two and two-thirds” of a cup, hour, or mile instead of just blurting out decimals. Mixed numbers make math feel more approachable.
How 8/3 Connects to Geometry
Dividing an 8-unit long object into 3 equal segments gives you pieces that are each 2.67 units long. This is useful in design, drafting, and construction, where symmetrical distribution is often required and precision can’t be compromised.
The Role of 8/3 in Data Science
Averages aren’t always clean whole numbers. If a machine processes 8 items every 3 seconds, the average speed is 2.67 items per second. These fractions help describe systems, trends, and behaviors in analytics, science, and business.
Educational Value in Learning 8/3
Students often first encounter improper fractions like 8/3 when learning to divide numbers that don’t break evenly. It’s a great example of mathematical thinking—understanding what to do when answers don’t come out “neat.”
Mental Math Trick for 8/3
To compute 8/3 mentally, divide 6 by 3 first (that’s 2), then divide the remaining 2 by 3 (which gives you about 0.666). Add them up to get 2.666. With this mental strategy, you can do quick estimates without a calculator.
8/3 in Programming and Code Logic
Some programming languages handle 8/3 differently depending on whether the numbers are defined as integers or floats. Integer division might return just 2, while float division returns 2.666…. This is crucial when writing precise calculations in code.
Relevance in Time Management
Imagine needing to split 8 hours of work across 3 projects. You’d need to spend about 2 hours and 40 minutes on each. That’s 8/3 hours per project. Understanding this helps with efficient time allocation.
Simplifying Improper Fractions Like 8/3
8/3 is already in its simplest form, but converting it to mixed numbers helps make it more digestible. Many practical tools—like recipe cards or spreadsheets—automatically format these for user clarity.
The Pattern of Repeating Decimals
Repeating decimals like 2.666… occur when the denominator of a fraction doesn’t evenly divide the numerator. Recognizing this helps build mathematical fluency and strengthens your number sense.
Financial Examples of Using 8/3
If $8 is to be shared among 3 people, each would get $2.67, with a cent left unaccounted for. This small rounding issue shows how even fractions like 8/3 can cause financial discrepancies when not handled carefully.
Scientific Precision and 8/3
In scientific calculations, approximating 8/3 to 2.67 might be enough—but in high-precision work like chemistry or physics, repeating decimals are used as-is for utmost accuracy. Every tiny decimal could impact results.
Cultural and Symbolic Interpretations
While rare, some numerologists and philosophers consider numbers like 2 2/3 (8/3) to represent balance and division. This is more poetic than practical, but it shows how even simple fractions can inspire abstract thought.
The Philosophical Side of Numbers Like 8/3
Think about it: something that can’t be written as a clean whole number teaches us that not everything fits perfectly. 8/3 becomes a small lesson in accepting imperfection, much like life itself.
Conclusion
8/3 might look like just another fraction, but it’s a powerhouse of usefulness. Whether you’re dividing up time, money, space, or ingredients, understanding this improper fraction helps you navigate daily life with precision and clarity. It’s not just about math—it’s about mastering small tools that make a big difference.
FAQs
Is 8/3 a rational number?
Yes, because it’s a ratio of two integers and can be written as a fraction.
How do I convert 8/3 into a mixed number?
8 divided by 3 equals 2 with a remainder of 2. So, it becomes 2 2/3.
Can 8/3 be used in cooking?
Absolutely. It’s commonly used in recipes where ingredients are split across portions.
What is the decimal form of 8/3?
It is 2.666…, a repeating decimal.
Why is 8/3 important in daily life?
It helps with splitting quantities evenly, estimating, budgeting, and more.